NMAT・JMATにおいては様々な種類の問題が出題され、その中でも特に集合問題、割合問題、推論問題などの数学問題は、コツがあります。
本記事では、NMAT・JMATの内容や対策について詳しく解説していきます。数学の苦手意識を払拭し、自信を持って試験に挑むための情報満載です。
NMAT・JMATについてより深く理解するための無料問題集や攻略法をお届けします。NMAT・JMATの攻略に役立つ情報をぜひチェックしてみてください。
結論:NMAT・JMATでオススメの解き方
- 集合:単純な2~3グループに分ける問題ならベン図が便利
- 割合:基本式 比べられる量/元の量=割合
- 損益:基本式 定価(売り値)=原価(仕入れ値)+利益
- 推論:問題文を絵や数式で書いてみる
- 確率:「少なくとも」は「1ー1回も〇〇しない確率」と読み替える
- 速度:みはじ(きはじ)で解こう
- 集合応用:ベン図の2つの円を近づけよう
- 図表読み取り:表の縦と横の関係を理解する
- グラフ読み取り:分母にどの数字を使うべきか、よく考えよう
- 工程表:工程表を書き出そう
- フローチャート:フローチャートと問題文のリンクを把握しよう
NMAT・JMATオススメの本
NMAT・JMATとは?
NMAT・JMATでは「能力」「性格」「指向」の3つの指標により適正が測定されます。NMAT・JMATの構成は下のようになります。
- 検査Ⅰ:言語能力適正検査(国語) 約30分
- 検査Ⅱ:非言語能力適正検査(数学) 約40分
- 検査Ⅲ:性格検査
- 検査Ⅳ:指向検査 Ⅲ,Ⅳ合わせて40分
この中でも「検査Ⅱ:非言語能力適正検査(数学)」は最も対策が必要です。数学のレベルは中学レベルの基礎知識を問われますが、難易度が高い問題も多く、制限時間がかなり短いので、問題を素早く理解し、素早く計算する高い能力が求められます。
以下のカテゴリからバランスよく出題されるので、それぞれの効率的な解き方をマスターしないと、高得点は難しいでしょう。
集合問題
【おすすめの解き方】単純な2~3グループに分ける問題ならベン図が便利
例題
30人のクラスでアンケートを取った。電車が好きと回答したのは10人。自動車が好きと回答したのは15人。電車も飛行機も好きだと回答したのは5人のとき、電車も飛行機も好きでないと回答した人は何人か?
ベン図とは、四角の中に、2つの円があり、2つの円の一部が重なり合った図です。中学校の数学で学んだのを覚えている人も多いのではないでしょうか?
ベン図を使うことで、問題文を整理整頓できるので、素早く問題が解けるようになります。
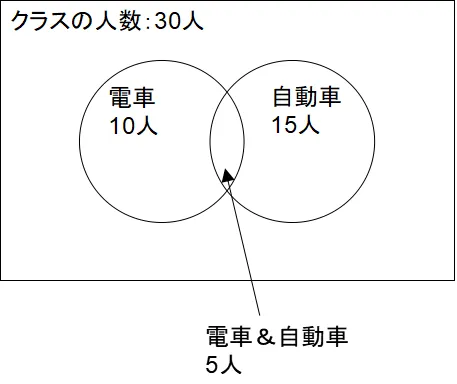
電車も自動車も好きではない人数 = 四角の面積(30人) – (2つの円の面積(左の円の面積(10人) + 右の円の面積(15人) – 重なり合った部分の面積(5人)) = 30 – ( 10+15 – 5 ) = 10人
答え:10人
もっと詳しく知りたい方はこちらからどうぞ
割合問題
【おすすめの解き方】割合の基本式 比べられる量/元の量=割合
例題
〇人の40%は550人である。
問題文に出てくる「比べられる量」を分子に、「元の量」を分母にすると、イコール割合になります。
- 比べられる量=550人
- 元の量=〇人
- 割合=40%=40/100
答え:〇=1375人
もっと詳しく知りたい方はこちらからどうぞ
損益問題
【おすすめの解き方】基本の式 定価(売り値)=原価(仕入れ値)+利益
例題
原価が5000円の商品を、利益が原価の10%のようになるように売るとき、定価はいくらか?
損益計算の問題を解くときに必要になる基本的な考え方はイラストのようになります。まずはこの基本的な考え方を、問題を解きながら抑えましょう。

- 定価 = 原価(5000円) + 利益(原価の10%)
ここで利益が原価の10%となりますが、原価は既に5,000円と分かっているので、利益はその10%の500円になります。
- 定価 = 原価(5,000円) + 利益(500円) = 5,500円
答え:5,500円
もっと詳しく知りたい方はこちらからどうぞ
推論問題
【おすすめの解き方】問題文を絵や数式で書いてみる
例題
A,B,C,Dの4人がテストを受けた。それぞれのテストの点数について以下のことが分かっているとき、Aの順位として考えられるのは何位か?考えれる順位をすべて挙げよ。
・4人の中に同じ点数はいない。
・Cの点数はAの点数より低い。
・Dの特典はAとBの平均に等しい。
・Bの点数はCの点数より高い。
例題を式で表すと以下のようになります。
- A≠B≠C≠D
- A>C
- D=(A+B)/2
- B>C
次にこの式から、考えれる順位のパターンを挙げていきます。まず着目したいのは2つ目と4つ目です。この2つの式が成り立つのは、以下のパターンです。
- A>B>C (Dの順位は不明)
- B>A>C (Dの順位は不明)
この2つの式から、A,B,Cの関係性を絞り込むことができました。次は3つ目の式から考えられる順位のパターンを挙げていきます。
- A>D>B (Cの順位は不明)
- B>D>A (Cの順位は不明)
今まで挙がって式を組み合わせて、A,B,C,Dの4つの順位を考えます。1つ目の式と3つ目の式を組み合わせた順位と、2つ目の式と4つ目の式を組み合わせた順位の2パターンが考えられます。
- A>D>B>C
- B>D>A>C
答え:1位と3位
もっと詳しく知りたい方はこちらからどうぞ
NMAT・JMATオススメの本
確率問題
【おすすめの解き方】「少なくとも」は「1ー1回も〇〇しない確率」と読み替える
例題
サイコロを2回連続で投げるとき、少なくとも1回は6が出る確率はいくらか?
サイコロを2回連続で投げて「少なくとも1回は6が出る」とは具体的にどんな状況でしょうか?整理してみましょう。
- 1回目に6が出て、2回目に6が出ないパターン
- 1回目に6が出て、2回目も6が出るパターン
- 1回目に6は出ないで、2回目に6が出るパターン
の3パターンになります。
この3パターンを考え直してみると、実は次のように言い換えることができます。
- 全てのパターンから、1回目も2回目の6が出ないパターンを除いたパターン
ここまで理解できますでしょうか?そうしたらもう少し考えを進めます。「全てのパターン」とはつまり100%のことです。100%を分数で表すと1になります。そして、その1から「1回目も2回目の6が出ないパターン」を除いた残りを求めるので、以下の式が成り立ちます。
- 少なくとも1回は6が出る = 1 – 1回も6が出ないパターン
それでは、これを使って計算していきましょう。「1回も6が出ないパターン」とは1回目も2回目も6以外の数字が出るパターンです。つまり以下のように計算できます。
- 1回も6が出ないパターン = 5/6 × 5/6 = 25/36
1からこの数字を引くと
- 1 – 25/36 = 36/36 – 25/36 = 11/36
答え:11/36
もっと詳しく知りたい方はこちらからどうぞ
速度問題
【おすすめの解き方】みはじ(きはじ)で解こう
小学生の頃、算数の授業で習ったのを覚えていますでしょうか?道のり(距離)、速さ、時間の計算をするときに、この「みはじ(きはじ)」の絵を書くと便利です。
の式.webp)
例題
時速65㎞の自動車で30分かかる距離を、分速250mの自転車で走ったとき、何時間何分かかるか?
まずは冒頭の「時速65㎞の自動車で30分かかる距離」を計算します。
- 距離 = 速さ × 時間
- 距離 = 時速65km × 30分
ここで、1つ注意点があります。
上の計算式の速さが「時速」になっていることに気づいたでしょうか?
時速とは「1時間でどのくらいの距離を進むかを表す言葉」です。つまり、時速を使って計算するときは、時間は何時間か?と単位を揃えて計算する必要があります。
上の計算式の30分を何時間か?で表すと「0.5時間」になります。つまり
- 距離 = 時速65km × 0.5時間
- 距離 = 37.5km
となります。
次に、問題文の後半の「分速250mの自転車で走ったとき、何時間何分かかるか」を計算します。
求めたい答えは「時間」です。
- 時間 = 距離 ÷ 速さ
- 時間 = 37.5km ÷ 分速250m
ここで、1つ注意点があります。
上の計算式で「km」と「m」が混在しています。
単位が混在したままでは正しい計算ができません。単位を揃えましょう。ここでは「m」に揃えてみたいと思います。
- 時間 = 37,500m ÷ 分速250m
- 時間 = 150
答え:150分
もっと詳しく知りたい方はこちらからどうぞ
集合応用問題
【おすすめの解き方】ベン図の2つの円を近づけよう
例題
100人に電車と車について質問をしたところ、電車が好きと回答したのは65人、車が好きと回答したのが70人いた。このとき両方とも好きと回答した人数は最大で何人か?
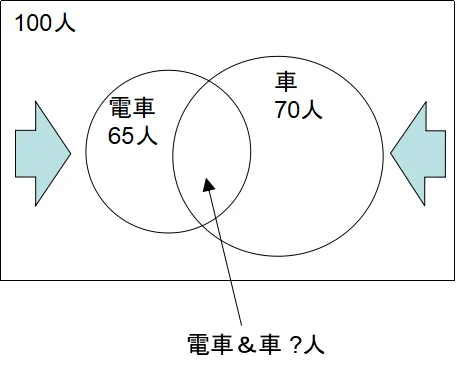
上のように、2つの円が近づくと、2つの円が重なり合う部分の面積が増えていきます。
そして、これが一番大きくなることを目的にどんどん近づけていきましょう。
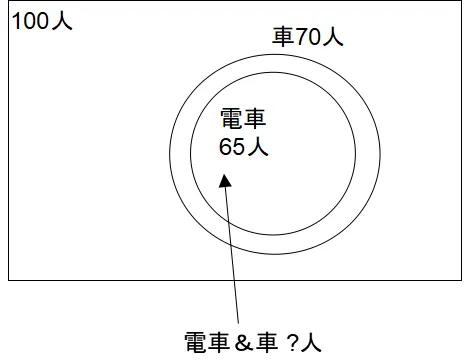
すると、上のように大きい円の中に小さい円がすっぽり入ってしまいました。
これが、2つの円が重なる部分の大きさが最大になった、つまり問題で問われている答えになります。
このとき、2つの円が重なる部分の大きさ=小さい円の大きさになります。つまり、答えは小さい円の大きさ=電車が好きと回答した人数となります。
答え:65人
もっと詳しく知りたい方はこちらからどうぞ
図表読み取り問題
【おすすめの解き方】表の縦と横の関係を理解する。
例題
あるクラスで、好きな食べ物についてのアンケートをしたところ、下の表のような結果になった。このとき、A~Cに入る数値を答えろ。

まず、縦の関係について考えてみましょう。一番上の行は食べ物の種類が書かれています。そして次の行が、それが好きだと回答した人の人数、そして最後の行が回答した人の割合です。
次に横の関係について考えてみましょう。左から2番目から5番目の列がアンケートへの回答結果です。一番右の列が、アンケートに回答した合計人数とその割合です。アンケートは50人に行われ、すべての人から回答を得られたので回答率は100%だということが分かります。
これを理解した上で、問題文を解いていきましょう。
まずはAです。Aが関連する横と縦の関係を注意深く観察しましょう。すると、横の関係から、以下の計算式が成り立つことが分かります。

- 15人+10人+20人+A=50人
- A=50人-15人-10人ー20人
- A=5人
これにより、表のAが埋まりました。

次にBについて考えてみましょう。Bが関連する横と縦の関係を注意深く観察しましょう。すると、縦と横の関係から、以下の計算式が成り立ちます。
- B=10/50
- B=0.2
- B=20%
これにより、表のBが埋まりました。

次にCについて考えてみましょう。Cが関連する横と縦の関係を注意深く観察しましょう。すると、横の関係から答えを求めることができます。

- 30%+20%+40%+C=100%
- C=100%-30%-20%-40%
- C=10%
別解)縦の関係から、以下の計算式で解いてもOKです。
- C=5/50
- C=0.1
- C=10%
答え: A=5人 B=20% C=10%
NMAT・JMATオススメの本
もっと詳しく知りたい方はこちらからどうぞ
グラフ読み取り問題
【おすすめの解き方】分母にどの数字を使うべきか、よく考えよう
例題
下のグラフはある企業の事業部別の売上を表している。
- 2019年から2020年のX事業部の売上は何%減少したか?
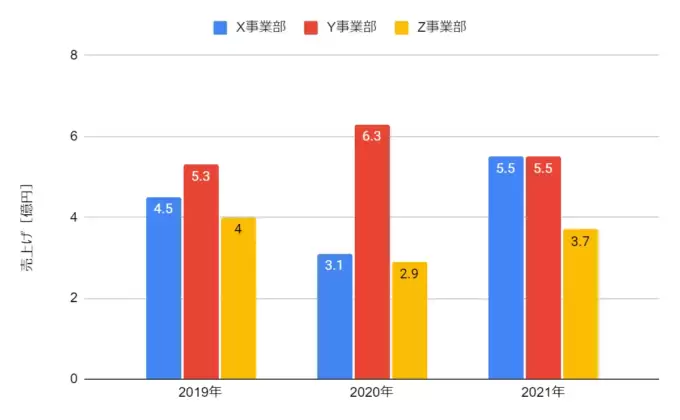
2019年と2020年での変化の割合が問われています。割合を答えるので分数を使うことは想像できると思います。ここで悩ましいのが「分母にどの数字を使うべきか」です。
問題文の「2019年から2020年の」とあります。これを言い換えると「2019年から”見て”、2020年はどのくらい変わったのか?」となります。
つまり、分母は「”2019年”のX事業部の売上」にすべきだということがわかります。
- 昨年からの減少率=減少値/昨年の値
- 昨年からの増加率=増加値/昨年の値
以上から、以下のように計算して行きます。
- 2019年から2020年の減少率=2019年から2020年の減少値/2019年の値
- 2019年から2020年の減少率=4.5億円-3.1億円/4.5億円
- 2019年から2020年の減少率=1.4億円/4.5億円=0.31=31%
答え:31%
もっと詳しく知りたい方はこちらからどうぞ
工程表問題
【おすすめの解き方】工程表を書き出そう
例題
ある製造工程はAからFの6つの作業から成り立っている。それぞれの作業には以下の条件がある
- 作業Cに取り掛かる前に作業Aが終わっていること
- 作業Dに取り掛かる前に作業AとBが終わっていること
- 作業Eに取り掛かる前に作業Dが終わっていること
- 作業Fに取り掛かる前に作業CとEが終わっていること
それぞれの作業日数は以下の通りである。
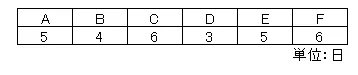
- 問:全作業が終了する最短日数は何日か?
横軸に作業日数を、縦軸にそれぞれの作業を並べます。問題文の条件に注意しながら日程表を作ると、以下のようになります。制約条件は矢印を使うと理解しやすいのでオススメです。
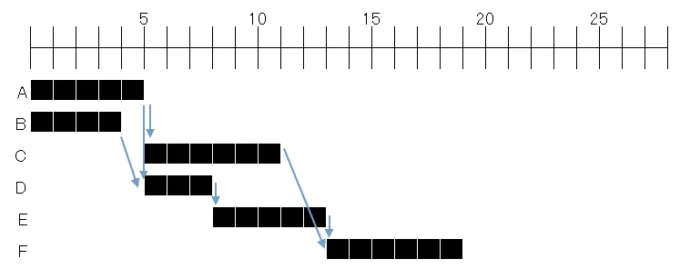
工程表の最後の作業の終了日を確認します。
答え:19日
もっと詳しく知りたい方はこちらからどうぞ
フローチャート問題
【おすすめの解き方】フローチャートと問題文のリンクを把握しよう
あるウェブサイトでは、800円の商品Xと、300円の商品Yを取り扱っている。合計金額が6000千円以上、もしくは合計個数が10個以上の場合に送料無料となる。それ以外は送料500円がかかる。下は、代金計算のフローチャートである。このとき、以下の質問に答えなさい。
- 問:Aに入る式はなにか?

問題文をフローチャートに当てはめると下の図のようになります。

問題文では「A」に入る式が問われています。上の図のとおりAには「合計個数が10個以上」を表す条件式を答えます。
答え: x + y ≧ 10
もっと詳しく知りたい方はこちらからどうぞ
まとめ
NMAT・JMATで時間切れにならず、効率的な解き方を全出題範囲11カテゴリの例題を使って紹介します。私が実際に昇進試験を受けて、攻略した経験を元に解説します。
結論:NMAT・JMATでオススメの解き方
- 集合:単純な2~3グループに分ける問題ならベン図が便利
- 割合:基本式 比べられる量/元の量=割合
- 損益:基本式 定価(売り値)=原価(仕入れ値)+利益
- 推論:問題文を絵や数式で書いてみる
- 確率:「少なくとも」は「1ー1回も〇〇しない確率」と読み替える
- 速度:みはじ(きはじ)で解こう
- 集合応用:ベン図の2つの円を近づけよう
- 図表読み取り:表の縦と横の関係を理解する
- グラフ読み取り:分母にどの数字を使うべきか、よく考えよう
- 工程表:工程表を書き出そう
- フローチャート:フローチャートと問題文のリンクを把握しよう
NMAT・JMATオススメの本

関連記事
NMAT・JMAT無料例題&解説_集合問題 時間切れ対策 (eezoublog.com)
NMAT・JMAT無料例題&解説_割合問題 時間切れ対策 (eezoublog.com)
NMAT・JMAT時間切れ対策 無料問題集&解説_推論問題 (eezoublog.com)
NMAT・JMAT時間切れ対策 無料問題集&解説_確率問題 (eezoublog.com)
NMAT・JMAT無料例題&解き方解説_集合応用問題_時間切れ対策 (eezoublog.com)
NMAT・JMAT時間切れ対策 無料例題&解説_図表の読み取り (eezoublog.com)
NMAT・JMAT時間切れ対策 無料例題&解説_グラフの読み取り (eezoublog.com)





