NMAT・JMAT無料例題＆解説_速度問題_時間切れ対策

NMAT・JMATで時間切れにならず、効率的な解き方を例題を使って紹介します。私が実際に昇進試験を受けて、攻略した経験を元に「速度・距離・時間」を例題で解説します。

NMAT・JMATとは？

NMATは「管理者適正検査」と呼ばれ、中間管理職への昇進試験で使われる検査方法です。JMATは「中堅社員適正検査」と呼ばれ、中堅社員への昇進試験や中途採用で使われる試験方法です。NMAT・JMATでは「能力」「性格」「指向」の3つの指標により適正が測定されます。NMAT・JMATの構成は下のようになります。

• 検査Ⅰ：言語能力適正検査(国語)　約30分
• 検査Ⅱ：非言語能力適正検査(数学)　約40分
• 検査Ⅲ：性格検査
• 検査Ⅳ：指向検査　Ⅲ,Ⅳ合わせて40分

この中でも「検査Ⅱ：非言語能力適正検査(数学)」は最も対策が必要です。数学のレベルは中学レベルの基礎知識を問われますが、難易度が高い問題も多く、制限時間がかなり短いので、問題を素早く理解し、素早く計算する高い能力が求められます。以下のカテゴリからバランスよく出題されるので、それぞれの効率的な解き方をマスターしないと、高得点は難しいでしょう。

NMAT・JMAT速度問題_初級

例題
スタート地点から680m離れた地点に2分で到着するためには、分速何mで走れば良いか？

ポイント
みはじ（きはじ）で解こう

小学生の頃、算数の授業で習ったのを覚えていますでしょうか？

道のり（距離）、速さ、時間の計算をするときに、この「みはじ（きはじ）」の絵を書くと便利です。

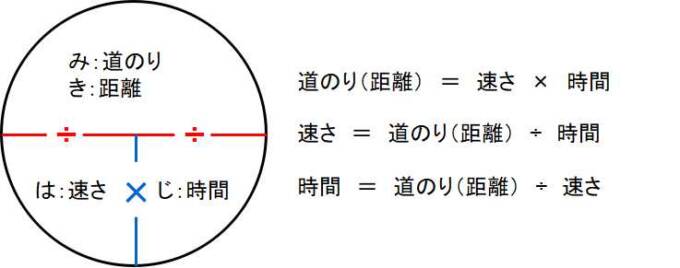
円の中の横棒は「÷」を、縦棒は「×」を意味します。求めたい答えを手で隠して、残りの２つとその間にある棒で、求めたい答えの計算方法がわかります。

さて、この問題の解き方を解説します。

求めたい答えは、分速なのでつまり「速さ」です。

• 速さ　＝　道のり（距離）　÷　時間
• 速さ　＝　680m　÷　2分
• 速さ　＝　分速340m

答え：分速340m

NMAT・JMAT速度問題_中級

例題
時速65㎞の自動車で30分かかる距離を、分速250mの自転車で走ったとき、何時間何分かかるか？

ポイント
時速＝時間、分速＝分　単位を揃えよう
km、m　単位を揃えよう

初級の問題よりも複雑になりましたが、心配することはありません。問題文の順番通りに計算していきましょう。

まずは冒頭の「時速65㎞の自動車で30分かかる距離」を計算します。

• 距離　＝　速さ　×　時間
• 距離　＝　時速65km　×　30分

ここで、１つ注意点があります。

上の計算式の速さが「時速」になっていることに気づいたでしょうか？

時速とは「1時間でどのくらいの距離を進むかを表す言葉」です。つまり、時速を使って計算するときは、時間は何時間か？と単位を揃えて計算する必要があります。

上の計算式の30分を何時間か？で表すと「0.5時間」になります。つまり

• 距離　＝　時速65km　×　0.5時間
• 距離　＝　37.5km

となります。

次に、問題文の後半の「分速250mの自転車で走ったとき、何時間何分かかるか」を計算します。

求めたい答えは「時間」です。

• 時間　＝　距離　÷　速さ
• 時間　＝　37.5km 　÷　分速250m

ここで、１つ注意点があります。

上の計算式で「km」と「m」が混在しています。

単位が混在したままでは正しい計算ができません。単位を揃えましょう。ここでは「m」に揃えてみたいと思います。

• 時間　＝　37,500m　÷　分速250m
• 時間　＝　150

答え：150分

NMAT・JMAT速度問題_上級

例題
自宅から5.5㎞離れた学校に行くのに、はじめは時速6㎞で歩き、途中から時速12㎞で走ったところ、合計で30分かかった。走っていたのは何分か？

ポイント
求めたい時間をXとしよう

この問題文の場合、途中まで歩いて、途中から走っています。そして走った時間が求めたい答えになります。

そこで、歩いた時間と、走った時間をそれぞれ以下のように設定しましょう。

• 歩いた時間：30 – X 分
• 走った時間：X 分

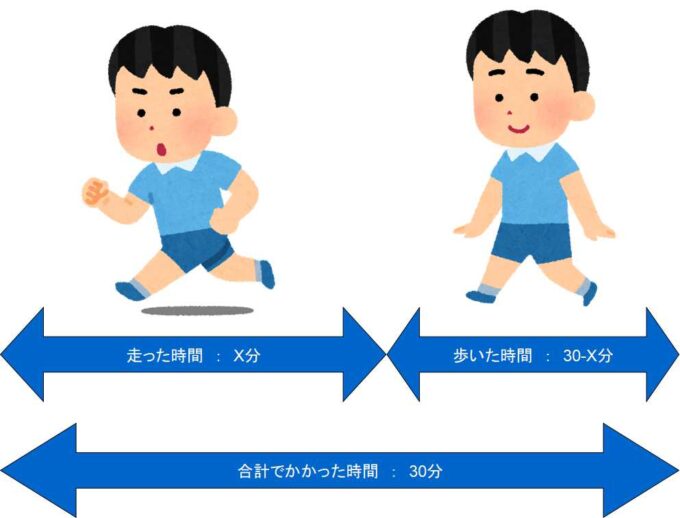
時間が決まったら、それぞれの距離を計算します。

• 歩いた距離　＝　時速6km　×　（30−X）分
• 走った距離　＝　時速12km　×　X分

このとき、速さは”時速”ですが、時間が”分”となっており、時間の単位があっていません。合わせましょう。

求めたい答えが”分”なので、時速を分速に変えたほうが計算が楽になります。

• 歩いた速さ　＝　時速6km ＝　分速6÷60km = 分速0.1km
• 走った速さ　＝　時速10km ＝　分速12÷60km = 分速0.2km

上の式のように、時速を分速に変えるには60で割り算します。これは1時間＝60分のため、1時間あたりの距離（時速）を60分割することで、1分間あたりの距離（分速）を求めることができるためです。

それでは、元の式の時速を分速にしてみましょう。

• 歩いた距離　＝　（時速6km→分速0.1km）　×　（30−X）分
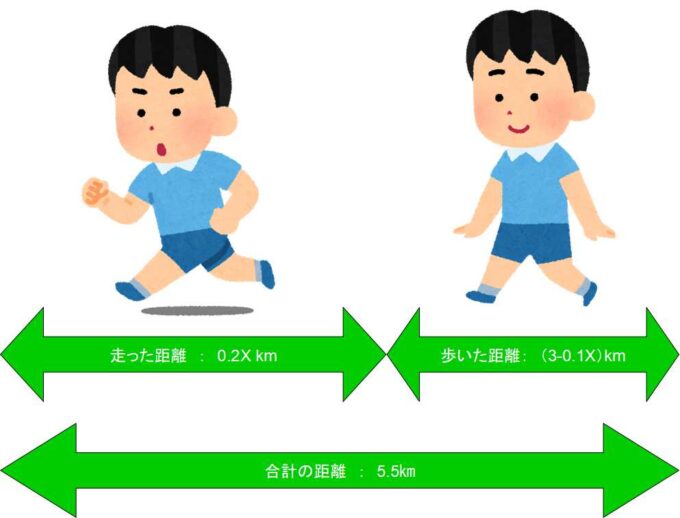
• 歩いた距離　＝　（3−0.1X）km

• 走った距離　＝　（時速12km→分速0.2km）　×　X分
• 走った距離　＝　0.2X km

計算されたそれぞれの距離を足し算すると5.5kmになります。

• 3 – 0.1X + 0.2X = 5.5
• 0.1X = 2.5
• X = 25

答え：走った時間は25分

まとめ：NMAT/JMAT速度問題の解き方

NMAT・JMATで時間切れにならず、効率的な解き方を例題を使って紹介します。私が実際に昇進試験を受けて、攻略した経験を元に「速度・距離・時間」を例題で解説します。